當(dāng)前位置:首頁 > 嵌入式培訓(xùn) > 嵌入式學(xué)習(xí) > 講師博文 > 棧及其應(yīng)用
 棧及其應(yīng)用
時間:2018-08-16 來源:未知
棧及其應(yīng)用
時間:2018-08-16 來源:未知
棧是限制在一端進(jìn)行插入操作和刪除操作的線性表(俗稱堆棧),允許進(jìn)行操作的一端稱為“棧頂”,另一固定端稱為“棧底”,當(dāng)棧中沒有元素時稱為“空棧”。向一個棧內(nèi)插入元素稱為是進(jìn)棧,push;從一個棧刪除元素稱為是出棧,pop。特點 :后進(jìn)先出(LIFO)。
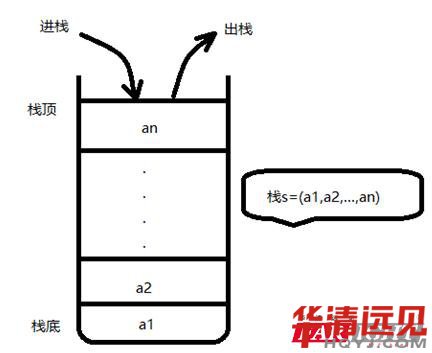
棧的存儲
棧的存儲方式分為順序存儲和鏈?zhǔn)酱鎯Α?/p>
棧的順序存儲結(jié)構(gòu)需要使用連續(xù)的存儲空間,并且需要一個元素來確定它的棧頂。利用數(shù)組來順序存儲棧中的所有元素,利用整型變量存儲棧頂元素的下標(biāo)位置,可以把這個變量稱為棧頂指針。
可以使用下面的結(jié)構(gòu)體來描述棧:
typedef int data_t;
#define SIZE 100;
struct Stack
{
data_t data[SIZE];
int top;
};
也可以使用動態(tài)分配內(nèi)存的辦法描述棧:
struct Stack
{
data_t * pData;
int top;
int maxSize;
};
top=-1表示棧空。
棧的鏈?zhǔn)酱鎯Y(jié)構(gòu)
棧的鏈?zhǔn)酱鎯Y(jié)構(gòu)是通過由結(jié)點構(gòu)成的單鏈表實現(xiàn)的。此時,表頭指針被稱為是棧頂指針,由棧頂指針指向的表頭結(jié)點被稱為是棧頂結(jié)點,整個單鏈表被稱為是鏈棧。對于鏈棧的入棧和出棧都是在表頭進(jìn)行。
可以使用下面的數(shù)據(jù)結(jié)構(gòu)來描述棧:
typedef int data_t;
struct stackNode
{
data_t data;
struct stackNode * pNext;
};
如果想要一個確定大結(jié)點數(shù)的鏈棧,可以將單鏈表的頭結(jié)點的數(shù)據(jù)域強轉(zhuǎn)為保存結(jié)點個數(shù)的值。頭結(jié)點指針域的值為NULL時,表示空棧。
棧的應(yīng)用
簡單應(yīng)用
1.輸入之后逆序輸出
2.語法檢查:括號匹配
每當(dāng)掃描到大中小的括號后,令其進(jìn)棧,當(dāng)掃描到右括號時,則檢查棧頂是否為相應(yīng)的左括號,若是,則出棧處理,若不是,則出現(xiàn)了語法錯誤。當(dāng)掃描到文件結(jié)尾,若棧為空則表明沒有發(fā)現(xiàn)括號配對錯誤。
3.數(shù)制轉(zhuǎn)換
十進(jìn)制轉(zhuǎn)八進(jìn)制。例如(1348)十進(jìn)制= (2504)八進(jìn)制,它基于如下的原理:
N N/8 N%8
1348 168 4
168 21 0
21 2 5
2 0 2
所以很明顯,N不斷的除8,每次的余數(shù)就是結(jié)果的其中一個因子,注意先出來的因子是低位的數(shù),可以考慮用棧來保存每次取余的結(jié)果,那么出棧的順序就是實際的結(jié)果順序。
代碼如下:
int decimalToOctonary(int decimalNumber)
{
double octNumber = 0;
int nCount = 0;
int nTemp = 0;
struct stack * pNumberStack;
//定義棧,pNumberStack并且初始化該棧 代碼略
pNumberStack = createStack();
while (decimalNumber)
{
nTemp = (int)decimalNumber%8;
//將nTemp入棧pNumberStack 代碼略
push(pNumberStack, nTemp);
decimalNumber = decimalNumber/8;
}
nCount = CountOfStack(numberStack);//元素個數(shù)也就是位數(shù)
while(!IsEmptyStack(numberStack))
{
//將棧numberStack中的元素出棧,并且賦值給nTemp 代碼略
pop(pNumberStack, &nTemp);
octNumber += (nTemp*pow(10.0, --nCount));
}
//銷毀棧numberStack
DestroyStack(&numberStack);
//返回轉(zhuǎn)換后的八進(jìn)制數(shù)
return (int)octNumber;
}
中綴和后綴表達(dá)式的轉(zhuǎn)換及計算
1.兩種表達(dá)式
中綴表達(dá)式:人使用的類似于(2+3*5),運算符號在數(shù)字中間的表達(dá)式。計算需要注意優(yōu)先級、括號這些問題,和運算符的實際運算次序往往同它們在表達(dá)式中的先后次序不一致,所以波蘭科學(xué)家提出了后綴表達(dá)式,把運算符放在兩個運算對象的后面。
在后綴表達(dá)式中看,不存在括號,也不存在運算符優(yōu)先級的差別,計算過程完全按照運算符出現(xiàn)的先后次序進(jìn)行,整個計算過程僅需掃描一遍便可完成。
2.中綴表達(dá)式轉(zhuǎn)換成后綴表達(dá)式的轉(zhuǎn)化規(guī)則和思路
利用棧,可以實現(xiàn)中綴表達(dá)式轉(zhuǎn)化為后綴表達(dá)式。也可以實現(xiàn)后綴表達(dá)式的計算。這里主要實現(xiàn)難度較大的中綴表達(dá)式向后綴表達(dá)式的轉(zhuǎn)化。中綴算術(shù)表達(dá)式轉(zhuǎn)換成對應(yīng)的后綴算術(shù)表達(dá)式的規(guī)則是:把每個運算符都移到它的兩個運算對象的后面,然后刪除掉所有的括號即可。
為了轉(zhuǎn)換正確,必須設(shè)定一個運算符棧,并在棧底存放一個特殊運算符,假定為’@’,讓它具有低的運算符優(yōu)先級,此棧用來保存掃描中綴表達(dá)式得到的暫不能放入后綴表達(dá)式中的運算符,等待它的兩個運算對象都放入到后綴表達(dá)式后,再令其出棧并寫入后綴表達(dá)式中。轉(zhuǎn)換的過程如下:
轉(zhuǎn)換過程如下:從頭到尾掃描中綴表達(dá)式,若遇到數(shù)字則直接寫入后綴表達(dá)式,若遇到運算符,則比較棧頂元素和該運算符的優(yōu)先級,當(dāng)該運算符的優(yōu)先級大于棧頂元素的時候,表明該運算符的后一個運算對象還沒有進(jìn)入后綴表達(dá)式,應(yīng)該把該運算符暫存于運算符棧中,然后把它的后一個運算對象寫入到后綴表達(dá)式中,再令其出棧并寫入后綴表達(dá)式中;若遇到的運算符優(yōu)先級小于等于棧頂元素的優(yōu)先級,表明棧頂運算符的兩個運算對象已經(jīng)被寫入后綴表達(dá)式,應(yīng)將棧頂元素出棧并寫入后綴表達(dá)式,對于新的棧頂元素仍進(jìn)行比較和處理,直到棧頂元素的優(yōu)先級小于當(dāng)前等待處理的運算符的優(yōu)先級為止,然后令該運算符進(jìn)棧即可。
按照上述過程掃描到中綴表達(dá)式的末尾,把剩余的運算符依次出棧并寫入后綴表達(dá)式即可。
(對于左括號直接進(jìn)棧,右括號則使左右兩個括號內(nèi)的運算符都出棧)。
后綴表達(dá)式求值
后綴表達(dá)式求值也需要一個棧,其元素類型為操作數(shù)的類型,此棧存儲后綴表達(dá)式中的操作數(shù)、計算過程的中間結(jié)果及后結(jié)果。
計算過程如下:掃描后綴表達(dá)式,若遇到操作數(shù)則進(jìn)棧,若遇到操作符則彈出兩個操作數(shù)進(jìn)行計算,然后將結(jié)果壓進(jìn)棧,直到后掃描完畢,棧中應(yīng)該保存著終結(jié)果。
以上是關(guān)于棧及棧的常見的應(yīng)用的一個總結(jié)。

